Kruskal’s Algorithm

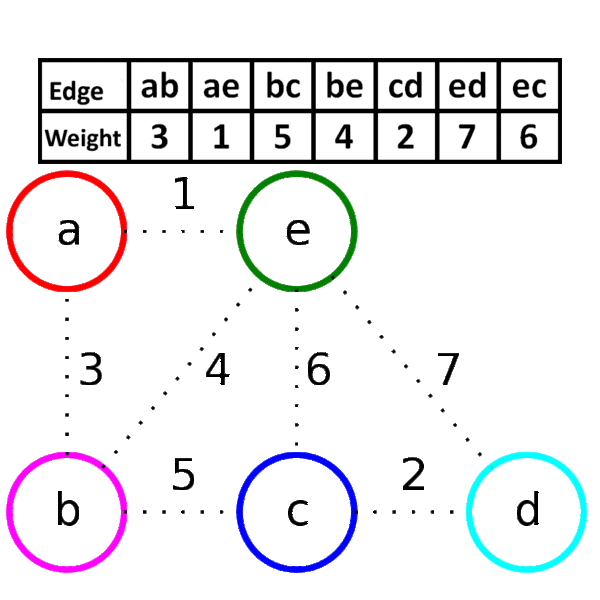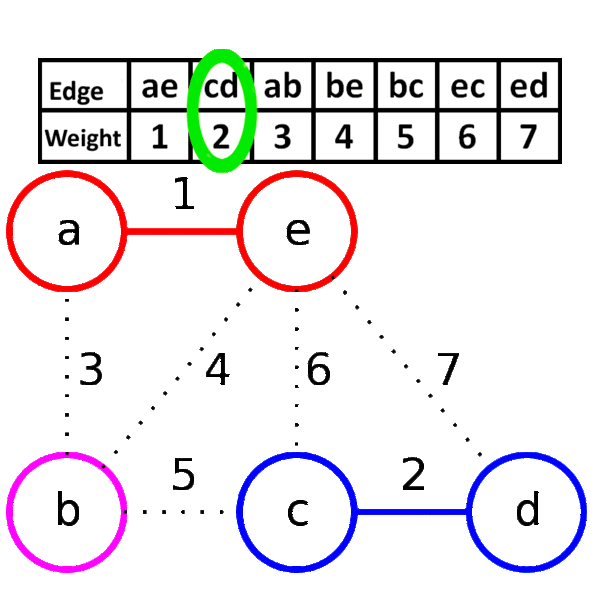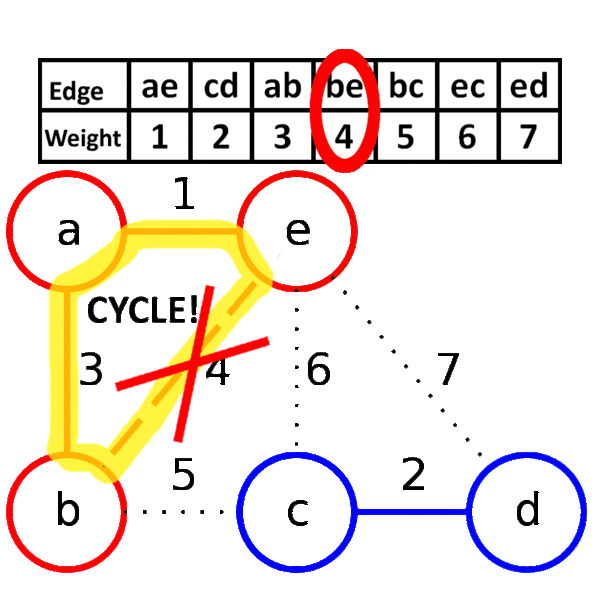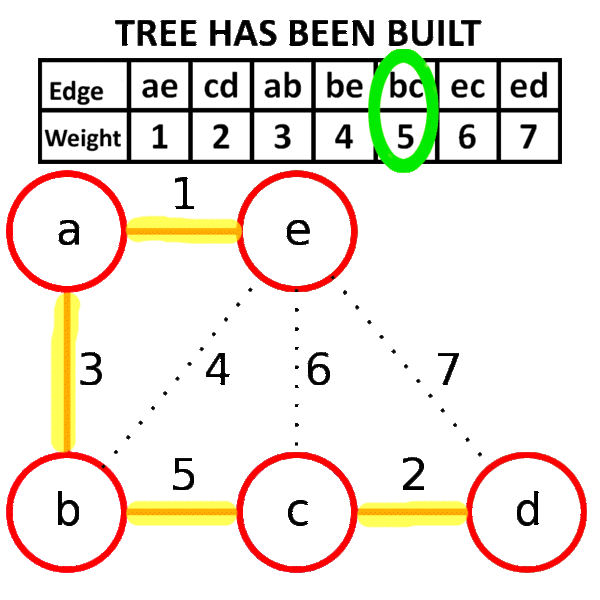
Kruskal’s algorithm is a greedy algorithm for solving the problem of finding a minimal spanning tree (MST) in a weighted and undirected graph. The goal is to find a subset of edges that will create a tree which contains all the original vertices, where the sum of the weights “Weighted graph” of all the edges in the tree is minimized.

Steps

• create a forest $F$ (a set of trees), where each vertex in the graph is a separate tree
• create a set $S$ containing all the edges in the graph
• while $S$ is nonempty and $F$ is not yet spanning
  • remove an edge with minimum weight from $S$
  • if the removed edge connects two different trees then add it to the forest $F$, combining two trees into a single tree

At the termination of the algorithm, the forest forms a minimum spanning forest of the graph. If the graph is connected, the forest has a single component and forms a minimum spanning tree.

Time Complexity

Time complexity mostly affected by sorting the edges at the beginning of the algorithm. In graph $G=(V,E)$ the time complexity is $O(|E| \cdot \log |V|)$ . If the edges of $G$ are pre-sorted then the time complexity is $O(|E| \cdot \alpha (|V|))$ and $ \alpha $ is the Ackermann function which measured as $ \alpha (n)≅O(1)$ .

Algorithm Pseudocode

Kruskal(G): // O(|E|log|V|)
    create Tree T ⇐ ∅

    for each v∈V(G) do: // O(|V|)
        MakeSet(v)
    end-for

    // sort E in increasing order by edges weight
    Sort(E(G)) // O(|E|log|V|)

    for each e∈E(G) do: // O(|E|)
        if FindSet(e.u) ≠ FindSet(e.v) then:
            T.add(e)
            Union(e.u, e.v) //𝑶(α(V)) ≅ 𝑶(𝟏)
        end-if
        if |E(T)| = |V(G)|-1 then:
            return T
        end-if
    end-for
    
    return T
    
end-Kruskal

MakeSet(v): // O(1)
    v.parent ⇐ v
end-MakeSet

FindSet(v): //𝑶(α(V)) ≅ 𝑶(𝟏)
    if v = v.parent then:
        return v.parent
    else:
        return FindSet(v.parent)
    end-if
end-FindSet

Union(u,v): //𝑶(α(V)) ≅ 𝑶(𝟏)
    uRoot ⇐ FindSet(u)
    vRoot ⇐ FindSet(v)
    uRoot.parent ⇐ vRoot
end-Union

Return the sum of weights of all the MST

SumOfMST(G):
    sum ⇐ 0
    T ⇐ Kruskal(G)

    for each e∈E(T) do: 
        sum ⇐ sum + e.weight
    end-for

    return sum
end-SumOfMST

Maximum Spanning Tree

MaximumSpanningTreeSum(G)

    for each e∈E(G) do:
        e.weight ⇐ (-1)*(e.weight)
    end-for

    T ⇐ Kruskal(G)
    sum ⇐ 0

    for each e∈E(T) do:
        e.weight ⇐ (-1)*(e.weight)
        sum ⇐ sum + e.weight
    end-for

    return sum
end-MaximumSpanningTreeSum

Java Code Version

public  class  Kruskal {  
  
	private Edge[] graph, tree;  
	private DisjointSets group;  
	private  int node_size, tree_size;  
	  
	public  Kruskal(Edge[] g) {  
	this.graph = new Edge[g.length];  
	  
	for(int i = 0; i < g.length; i++) {  
		graph[i] = new Edge(g[i].v, g[i].u, g[i].weight);  
	}  
	node_size = 0;  
	tree_size = 0;  
	for(Edge edge : graph) {  
		if(edge.v > node_size) node_size = edge.v;  
		if(edge.u > node_size) node_size = edge.u;  
	}  
	node_size++;  
	  
	group = new DisjointSets(node_size);  
	tree = new Edge[node_size-1];  
	  
	for (int i = 0; i < node_size; i++) {  
		group.make_set(i);  
	}  
		findMTS();  
	}  
	  
	private  void  findMTS() {  
		Arrays.sort(graph); // O(|E|log|E|)  
		for(Edge edge : graph) {  
			if(tree_size < node_size-1) {  
				if(group.union(edge.v, edge.u)) {  
				tree[tree_size++] = edge;  
				}  
			}  
			else {  
			break;  
			}  
		}  
	}  
	  
	public Edge[] getTree() {  
	return  this.tree;  
	}  
	  
	/***************************************************  
	* DisjointSets CLASS! *****************************  
	*/  
	public  static  class  DisjointSets {  
		private  int[] parent, rank; //rank[k]>=height of tree number k  
		  
		public  DisjointSets(int length) {  
		parent = new  int[length];  
		rank = new  int[length];  
		}  
		public  void  make_set(int k) {  
		parent[k] = k;  
		rank[k] = 0;  
		}  
		public  boolean  union(int v, int u) {  
		int root_v = find(v);  
		int root_u = find(u);  
		  
		if(root_v == root_u) { // if its equals = there is a circle.  
		return  false;  
		}  
		else {  
		if (rank[root_u] > rank[root_v]) {  
		parent[root_v] = root_u;  
		} else  if (rank[root_v] > rank[root_u]) {  
		parent[root_u] = root_v;  
		} else {  
		parent[root_v] = root_u;  
		rank[root_u]++;  
		}  
		return  true;  
		}  
	}  
	public  int  find(int v) {  
	if(parent[v] != v) {  
	parent[v] = find(parent[v]);  
	}  
	return parent[v];  
	}  
	}  
	/***************************************************  
	* EDGE CLASS! *************************************  
	*/  
	public  static  class  Edge  implements  Comparable<Edge> {  
		int v, u, weight;  
		public  Edge(int v, int u, int weight) {  
			this.v = v;  
			this.u = u;  
			this.weight = weight;  
		}  
		@Override  
		public String toString() {  
			return  "{" +  
			"v=" + v +  
			", u=" + u +  
			", weight=" + weight +  
			'}';  
		}  
		@Override  
		public  int  compareTo(Edge o) {  
			return Integer.compare(this.weight,o.weight);  
		}  
	}  
}